数据结构与算法

内存中的栈和堆

栈由操作系统自动分配释放，存放函数的参数值，局部变量的值等。其操作方式类似于数据结构中的栈。

堆由程序员分配释放，若程序员不释放，程序结束时可能由OS回收，分配方式类似于链表。

栈使用的是一级缓存，在被调用时处于存储空间中，调用完毕立即释放。

堆则是存放在二级缓存中，生命周期由虚拟机的垃圾回收算法来决定（并不是一旦成为孤儿对象就能被回收）。所以调用这些对象的速度要相对来得低一些。

与堆相比，栈存取速度比堆要快，仅次于直接位于CPU中的寄存器。缺点是存在栈中的数据大小与生存期必须是确定的，缺乏灵活性。

二分查找

输入一个有序元素列表，从1/2处开始查找，通过比较大小排除一半元素，再从剩下的元素的1/2处开始查找，不断递归，直到查找到结果为止。

复杂度为O(log n)

数组和链表

链表的每一个元素都存储了下一个元素的地址，从而使一系列随机的内存地址串联起来。

在链表中添加元素只需将其放入内存，并将其地址存储到前一个元素中。

从链表中读取元素时，需要从第一个元素开始，依次往下访问，直到找到对应元素为止，所以读取元素效率较低。

数组中的元素在内存中紧连在一起，所以从数组中随机的读取元素，只需要根据其索引值和起始地址做简单的算术运算即可。但是在数组中插入元素，就需要将要插入位置之后的元素依次后移，然后再讲元素插入，所以其插入效率较低。

数组和链表的操作运行时间对比如下：

操作	数组	链表
读取	O(1)	O(n)
插入	O(n)	O(1)
删除	O(n)	O(1)

选择排序

依次找到最小值，并将最小值与对应位置的元素交换

复杂度为O(n2)

function selectionSort(arr) {
    let length = arr.length,
        minIndex, temp;
        
    for (var i = 0; i < length - 1; i++) {
        minIndex = i;
        for (var j = i + 1; j < len; j++) {
            if (arr[j] < arr[minIndex]) {     // 寻找最小的数
                minIndex = j;                 // 将最小数的索引保存
            }
        }
        temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
    return arr;
} 

栈

栈是一种后进先出的列表，只有压入(push)和弹出(pop)两种操作。

递归

递归是一种函数自己调用自己解决方案，能用递归解决的问题都能用循环解决，递归并不是性能上的提升，而是更清晰，更容易理解。

递归都有基线条件和递归条件。

分治

分治算法divide and conquer，D & C，是一种著名的递归式问题解决方法。

归并排序

归并排序是将原始数组切分成较小的数组，直到每个小数组只有一个位置，接着将小数组归并成较大的数组，直到最后只有一个排序完毕的大数组。复杂度为O(nlog(n))

function mergeSort(array){
    const {length} = array
    if(length < 2) return array

    const middle = Math.floor( length / 2 )
    const left = mergeSort(array.slice(0, middle))
    const right = mergeSort(array.slice(middle, length))

    return merge(left, right)
}

function merge(left, right){
    let i = 0;
    let j = 0;
    const result = []

    while(i < left.length && j < right.length){
        const leftItem = left[i]
        const rightItem = right[j]
        let item

        if(leftItem < rightItem){
            item = leftItem;
            i++;
        }else{
            item = rightItem;
            j++;
        }
        result.push(item)
    }

    return result.concat(i < left.length ? left.slice(i) : right.slice(j))
}

快速排序

快速排序是一种常用的排序算法，复杂度为O(nlog n)，且性能比其他复杂度为O(nlog n)的排序算法好。

具体步骤如下：

1. 从数组中选择中间一项作为基准值
2. 划分，将数组分为大于基准值和小于基准值的两个数组
3. 递归，递归上面划分的两个数组，知道所有都只有一个元素

根据划分的过程是否需要额外的内存，又可将其分为in-place(原地算法)和out-place两种

out-place

function quickSort(arr) {
    //如果为空数组或者只有一个元素的数组，直接返回，递归的基线条件
    if(arr.length < 2) return arr;

    let pivotIndex = Math.floor( arr.length / 2 ),
        pivot = arr.splice(pivotIndex, 1)[0],
        left = [],
        right = [];

    for (let index = 0; index < arr.length; index++) {
        const item = arr[index];
        
        if (item < pivot){
            left.push(item)
        }else{
            right.push(item)
        }
    }

    console.log('quickSort', 'pivot', pivot, 'pivotIndex', pivotIndex, 'left', left, 'right', right);
    
    left = quickSort(left);
    right = quickSort(right);

    return [...left, pivot, ...right]
}

in-place

function quickSort(arr) {
    sortByIndex(arr, 0, arr.length - 1);

    return arr
}

function sortByIndex(arr, left, right) {
    if(arr.length < 2) return;

    var pivotIndex = partition(arr, left, right); //基准值的索引值

    console.log('pivotIndex', pivotIndex);

    left < pivotIndex - 1 && sortByIndex(arr, left, pivotIndex - 1); //对索引值左边的元素进行排序
    pivotIndex < right && sortByIndex(arr, pivotIndex, right); //对索引值右边的元素进行排序
}

function partition(arr, left, right){
    let pivotIndex = Math.floor((left + right) / 2), //基准值的索引值为两者中间的元素
        pivot = arr[pivotIndex],
        i = left,
        j = right; //基准值

    let tmp = arr.slice(left, right - left + 1);

    while (i <= j) {
        while (arr[i] < pivot) {
            i ++;
        }
        while (arr[j] > pivot) {
            j --;
        }
        if(i <= j){
            swop(arr, i, j);
            i++;
            j--;
        }
    }

    console.log('sub arr', tmp, 'after', arr.slice(left, right - left + 1), 'pivotIndex', i, 'init pivotIndex', pivotIndex);
    
    return i
}

function swop(arr, a, b){
    let tmp = arr[a];

    console.log('swop', a, b);
    
    arr[a] = arr[b];
    arr[b] = tmp;
    // console.log(arr);
}

散列表

树

树是一种分层数据的抽象模型。一个树结构包含一系列存在父子关系的节点。每个节点都有一个父节点（除了顶部的第一个节点）以及零个或多个子节点。位于树顶部的节点叫作根节点。树中的每个元素都叫作节点，节点分为内部节点和外部节点。至少有一个子节点的节点称为内部节点。没有子元素的节点称为外部节点或叶节点。

子树由节点和它的后代构成。节点的一个属性是深度，取决于它的祖先节点的数量。树的高度取决于所有节点深度的最大值。

二叉树

二叉树中的节点最多只能有两个子节点：一个是左侧子节点，另一个是右侧子节点。这些定义有助于我们写出更高效的向/从树中插入、查找和删除节点的算法。

二叉搜索树（BST）是二叉树的一种，它只允许在左侧节点存储（比父节点）小的值，在右侧节点存储（比父节点）大（或者等于）的值。

遍历一棵树是指访问树的每个节点并对它们进行某种操作的过程。访问树的所有节点有三种方式：中序、先序和后序。

自平衡树

AVL(Adelson-Velskii-Landi)树是一种自平衡二叉搜索树，任何一个节点左右两侧子树的高度之差最多为1。添加或移除节点时，会尝试保持自平衡。

红黑树

红黑树(Red-Black Tree, RBT)也是一个自平衡二叉搜索树。每个节点都遵循以下规则：

1. 每个节点不是红的就是黑的
2. 树的根节点是黑的
3. 所有叶节点都是黑的（用NULL引用表示的节点）
4. 如果一个节点是红的，那么它的两个子节点都是黑的
5. 不能有两个相邻的红节点，一个红节点不能有红的父节点或子节点
6. 从给定的节点到它的后代节点（NULL叶节点）的所有路径包含相同数量的黑色节点

图

图的相关概念

一个图G=(V, E)由以下元素组成：

• V: 一组顶点
• E: 一组边，连接V中的顶点

由一条边连接在一起的顶点称为相邻顶点。例如C和D是相邻的。

一个顶点的度是其相邻顶点的数量。例如A的度是3。

路径是顶点v1, v2, …, vk的一个连续序列，其中vi和vi+1是相邻的。例如路径ABEI。简单路径要求不包含重复的顶点。除去最后一个顶点，环(ADCA)也是一个简单路径。

如果图中不存在环，则称该图是无环的。如果图中每两个顶点间都存在路径，则该图是连通的。

图可以是无向的（边没有方向，无向图）或是有向的（有向图）。有向图如下图所示：

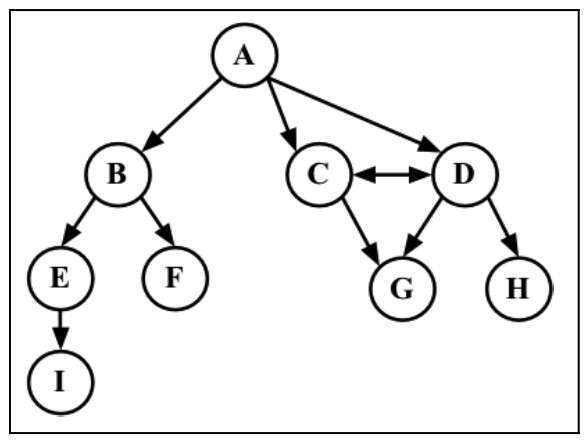
如果图中每两个顶点间在双向上都存在路径，则该图是强连通的。例如，C和D是强连通的。

图还可以是未加权的或是加权的。加权图的边被赋予了权值，如下图所示：

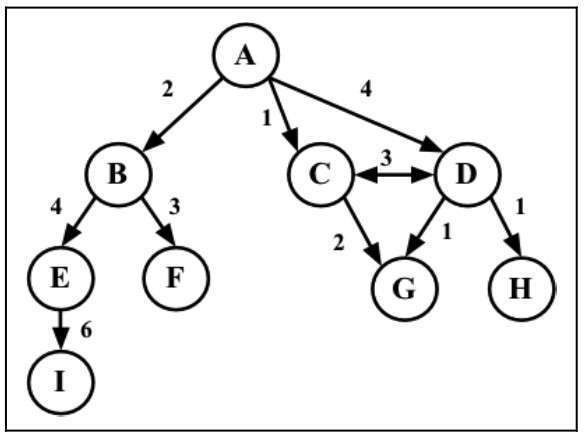
图的表示

邻接矩阵

图最常见的实现是邻接矩阵。每个节点都和一个整数相关联，该整数将作为数组的索引，用一个二维数组来表示顶点之间的连接。如果索引为i的节点和索引为j的节点相邻，则array[i][j] === 1，否则array[i][j] === 0。

不是强连通的图（稀疏图）用邻接矩阵来表示，矩阵中将会有很多0，会对存储空间造成一定的浪费。

邻接表

还可以用一种叫作邻接表的动态数据结构来表示图。邻接表由图中每个顶点的相邻顶点列表所组成。可以用列表（数组）、链表，甚至是散列表或是字典来表示相邻顶点列表。邻接表对大多数问题来说都是更好的选择。

关联矩阵

还可以用关联矩阵来表示图。在关联矩阵中，矩阵的行表示顶点，列表示边。使用二维数组来表示两者之间的连通性，如果顶点v是边e的入射点，则array[v][e] === 1；否则，array[v][e] === 0。关联矩阵通常用于边的数量比顶点多的情况。

广度优先搜索

加权图与狄克斯特拉算法

贪心算法

贪心算法基础概念

狭义的贪心算法指的是解最优化问题的一种特殊方法，解决过程中总是做出当下最好的选择，因为具有最优子结构的特点，局部最优解可以得到全局最优解；这种贪心算法是动态规划的一种特例。能用贪心解决的问题，也可以用动态规划解决。

而广义的贪心指的是一种通用的贪心策略，基于当前局面而进行贪心决策。

贪心算法的思考过程

贪心的思考过程类似动态规划，依旧是两步：大事化小，小事化了。

大事化小：

一个较大的问题，通过找到与子问题的重叠，把复杂的问题划分为多个小问题；

小事化了：

从小问题找到决策的核心，确定一种得到最优解的策略。

斐波那契数列计算

递归

缺点，随着n的变大，执行次数大量增长

function getFibonacci(n){
    if(n < 3){
        return 1
    }else{
        return getFibonacci(n - 1) + getFibonacci(n - 2)
    }
}

动态规划

通过一个数组保存中间结果，通过循环计算斐波那契数列，并将最后的值返回。 动态规划算法需要将中间结果保存起来。

//方案一
function getFibonacci(n){
    if (n === 1 || n === 2){
        return 1
    }else{
        let tmp = [1, 1];

        for(let i = 2; i <= n; i ++){
            tmp[i] = tmp[i - 1] + tmp[i - 2]
        }

        return tmp[n - 1]
    }
}

//方案二
function getFibonacci(n){
    if (n === 1 || n === 2){
        return 1
    }else{
        let last = 1,
            second = 1,
            tmp;

        for(let i = 2; i <= n; i ++){
            tmp = last;
            last = last + second;
            second = tmp;
        }

        return last
    }
}

算法复杂度

大O表示法

大O表示法用于描述算法的性能和复杂程度。将算法按照消耗的时间进行分类，依据随输入增大所需要的空间/内存。

常用的函数有：

符号	名称
O(1)	常数的
O(log(n))	对数的
O(log(n))c	对数多项式的
O(n)	线性的
O(n2)	二次的
O(nc)	多项式的
O(cn)	指数的